3 Decomposição de séries temporais e modelos clássicos

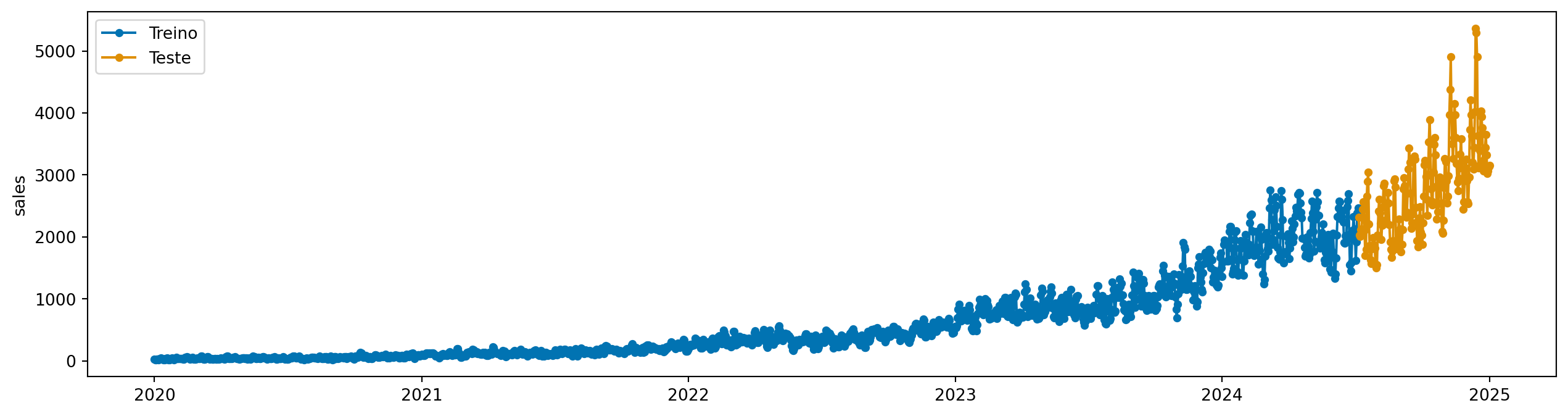
Nesse capítulo, vamos começar a usar um dataset mais realista, com dados simulando vendas diárias de uma empresa de varejo.

Vamos aprender os seguintes pontos:

Definição de séries integradas, e uso de diferenciação
Modelos estatísticos clássicos: modelos de suavização exponencial e modelos autoregressivos (AR)
Como usar esses modelos com a biblioteca sktime

3.1 Importando dados

Para acessar os dados, vamos usar a classe SyntheticRetail da biblioteca tsbook, que contém dados simulados de vendas diárias de uma empresa de varejo.

from tsbook.datasets.retail import SyntheticRetail
from sktime.utils.plotting import plot_series

dataset = SyntheticRetail("univariate")
y_train, y_test = dataset.load("y_train", "y_test")

plot_series(y_train, y_test, labels=["Treino", "Teste"])

Os dados são diários, e vemos que sempre positivos. Também notamos que existe alguma sazonalidade, aparentemente algo mensal e anual, que aumenta de magnitude ao longo do tempo.

Algo que deve chamar a atenção nesse gráfico é que a magnitude da série temporal está aumentando ao longo do tempo. Isso não deve passar desapercebido, pois é um ponto importante para entendermos o que vem a seguir.

3.2 Auto-correlação

É interessante entender o quanto de informação o passado de uma série temporal carrega sobre o seu futuro. Uma maneira de capturar essa relação (considerando variações lineares) é através da auto-correlação. A autocorrelação para um determinado lag \(k\) é definida como:

\[ \text{Corr}(Y_t,Y_{t-k})=\frac{\text{Cov}(Y_t,Y_{t-k})}{\sqrt{\text{Var}(Y_t)\text{Var}(Y_{t-k})}} = \frac{E[(Y_t - \mu)(Y_{t-k} - \mu)]}{\sqrt{\text{Var}(Y_t)\text{Var}(Y_{t-k})}} \]

Em outras palavras, quando o valor em \(k\) observações atrás está acima (ou abaixo) da média, o valor atual também tende a estar acima (ou abaixo) da média?

Com plot_correlations, podemos visualizar algumas informações úteis:

No plot superior, vemos a série temporal original.
No canto inferior esquerdo, temos o gráfico de autocorrelação (ACF), que mostra a correlação entre a série temporal e suas versões defasadas (lags). Valores próximos de 1 ou -1 indicam uma forte correlação positiva ou negativa, respectivamente.
No canto inferior direito, temos o gráfico de autocorrelação parcial (PACF), que mostra a correlação entre a série temporal e suas versões defasadas, controlando para as correlações intermediárias. É útil para entender o efeito isolado de um lag.

from sktime.utils.plotting import plot_correlations


fig, ax = plot_correlations(y_train, lags=60)
fig.show()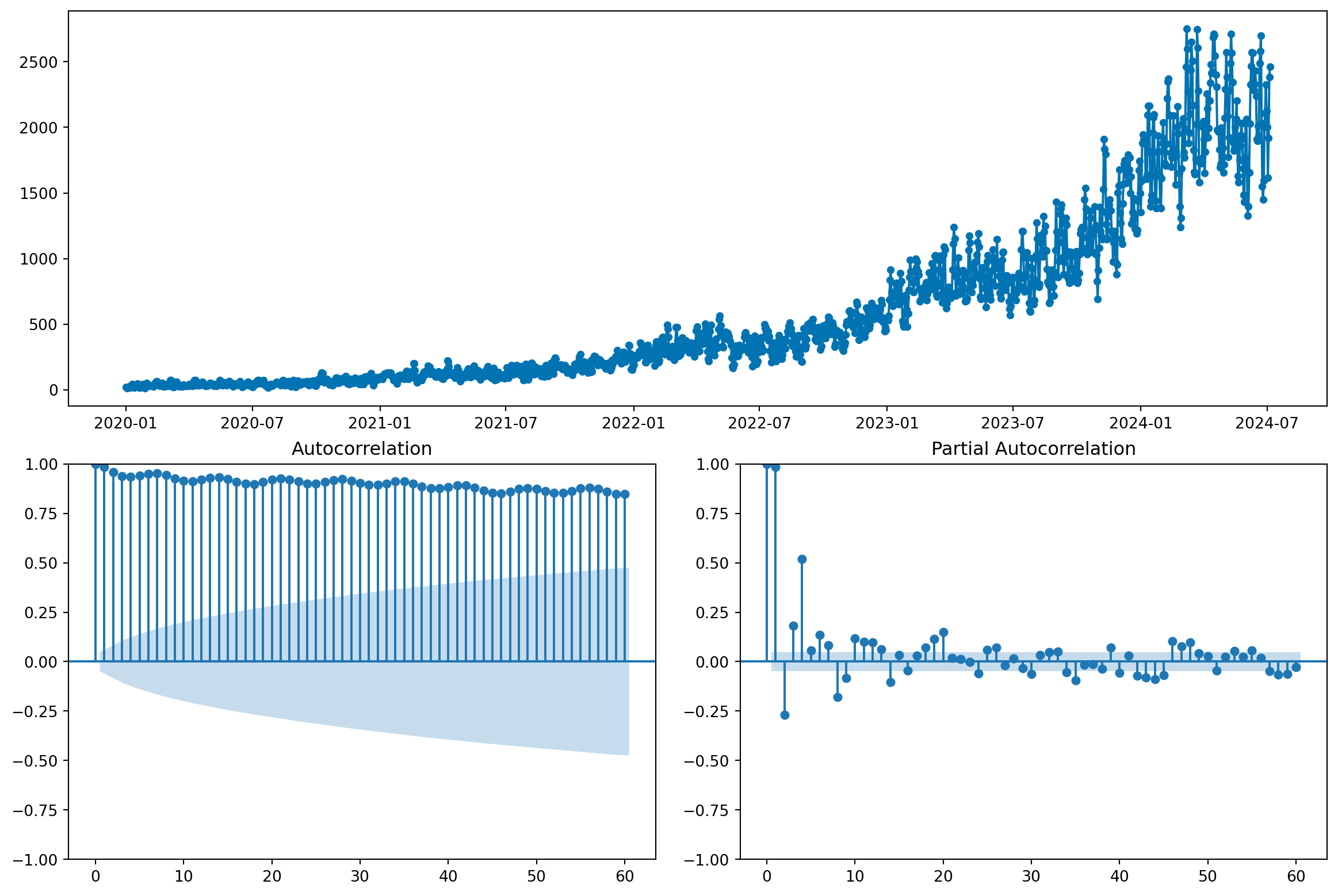

No gráfico de autocorrelação, vemos algumas características interessantes:

Valores são extremamente altos, e decaem lentamente ao longo do tempo.
Existem oscilações claras, indicando padrões sazonais na série temporal.

Tip

É um erro comum usar a correlação de lags de uma série para seleção de variáveis (lags). Sempre que possível, devemos eliminar a tendência antes de analisar a autocorrelação.

Veremos que esses padrões são indicativos de que a série temporal possui componentes importantes, e que valores passados dizem muito sobre valores futuros.

3.3 Componentes de séries temporais

Séries temporais podem ser decompostas em 3 componentes principais:

Tendência: padrão de longo prazo na série temporal
Sazonalidade: padrões que se repetem em intervalos regulares, como diariamente, semanalmente ou anualmente
Ruído: variação aleatória que não pode ser explicada pelos outros componentes

Uma série aditiva pode ser representada como:

\[ Y(t) = T(t) + S(t) + R(t) \]

onde \(T(t)\) é a tendência, \(S(t)\) é a sazonalidade, e \(R(t)\) é o ruído.

Em séries aditivas, o impacto da sazonalidade se dá em termos absolutos, dizemos: “em janeiro, as vendas aumentam em 100 unidades com relação a média do ano”.

Mas também existem séries multiplicativas, onde os componentes interagem de forma diferente:

\[ Y(t) = T(t) \cdot S(t) \cdot R(t) \]

Nessas séries, o impacto da sazonalidade se dá em termos relativos, dizemos: “em janeiro, as vendas aumentam em 20% com relação a média do ano”. Esse é o caso mais comum para séries não-negativas, como vendas. Isso vem por definição: se temos vendas muito baixas, por exemplo, 10 unidades, não faz sentido dizer que em janeiro as vendas diminuem em 100 unidades, pois isso levaria a vendas negativas. Já dizer que as vendas diminuem em 20% é perfeitamente razoável.

Tip

Em alguns casos, as séries multiplicativas são definidas como:

\[ Y(t) = T(t) + T(t) \cdot S(t) + T(t) \cdot R(t) \]

Quando a série é multiplicativa, podemos fazer recurso ao logaritmo para transformá-la em aditiva:

\[ log(Y(t)) = log(T(t)) + log(S(t)) + log(R(t)) \]

Para fazer isso no sktime, usamos o transformador LogTransformer. Transformadores são usados para pré-processar ou pós-processar os dados antes de aplicar um modelo de previsão, e sua interface é similar a dos modelos de previsão:

__init__: define os hiperparâmetros do transformador
fit: aprende os parâmetros do transformador a partir dos dados
transform: aplica a transformação nos dados
inverse_transform (opcional): aplica a transformação inversa nos dados

from sktime.transformations.series.boxcox import LogTransformer
log_transformer = LogTransformer()
log_transformer.fit(y_train)

LogTransformer()

Please rerun this cell to show the HTML repr or trust the notebook.

y_train_log = log_transformer.transform(y_train)
plot_series(y_train_log, labels=["Logaritmo"])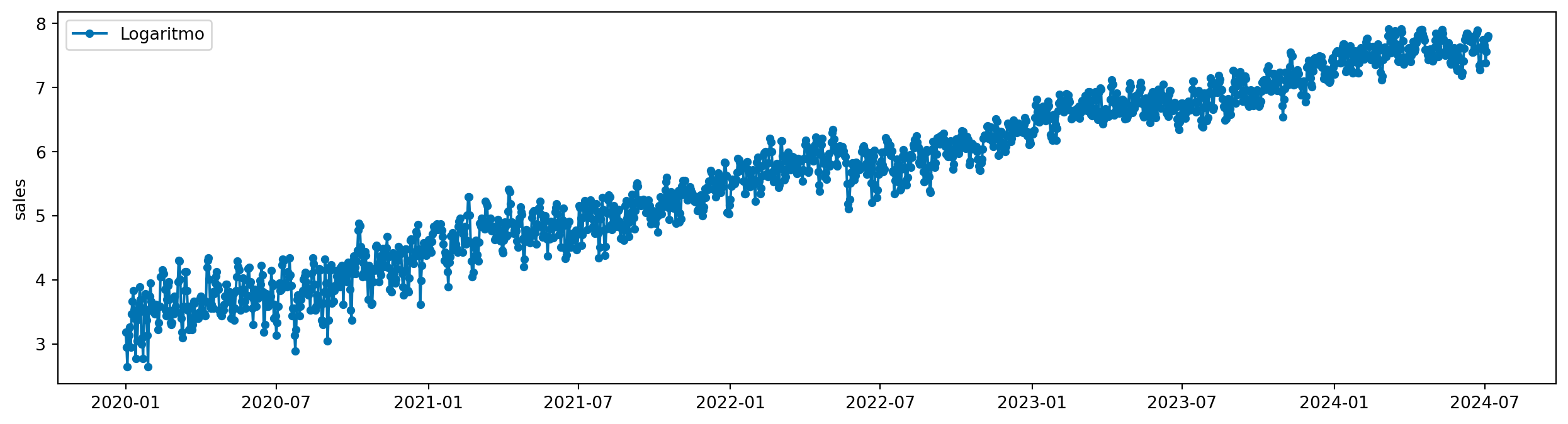

Ainda que não esteja perfeito, essa transformação estabiliza as variações da série temporal, o que é importante para alguns modelos de previsão.

3.3.1 Decompondo a série temporal

Sktime fornece algumas opções para decompor séries temporais. Aqui, vamos usar o Detrender para remover a tendência, e o Deseasonalizer para remover a sazonalidade.

3.3.1.1 Tendência

from sktime.transformations.series.detrend import Detrender, Deseasonalizer


detrender = LogTransformer() * Detrender(model="additive")
detrender.fit(y_train)
y_train_detrended = detrender.transform(y_train)
plot_series(y_train_detrended, labels=["Detrended"])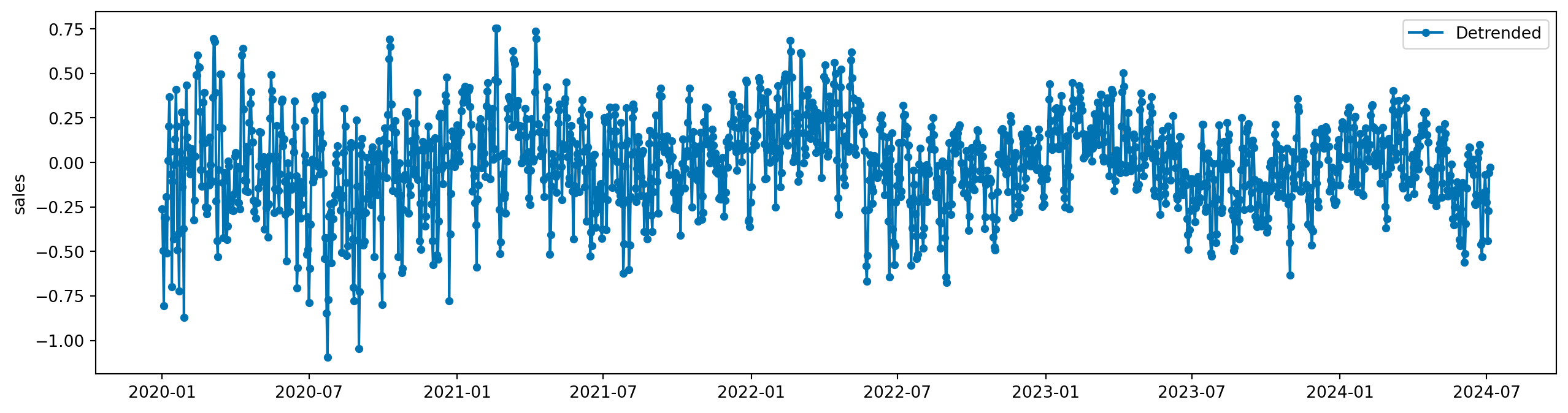

Vemos uma mudança importante no gráfico de autocorrelação:

fig, _ = plot_correlations(y_train_detrended, lags=60)
fig.show()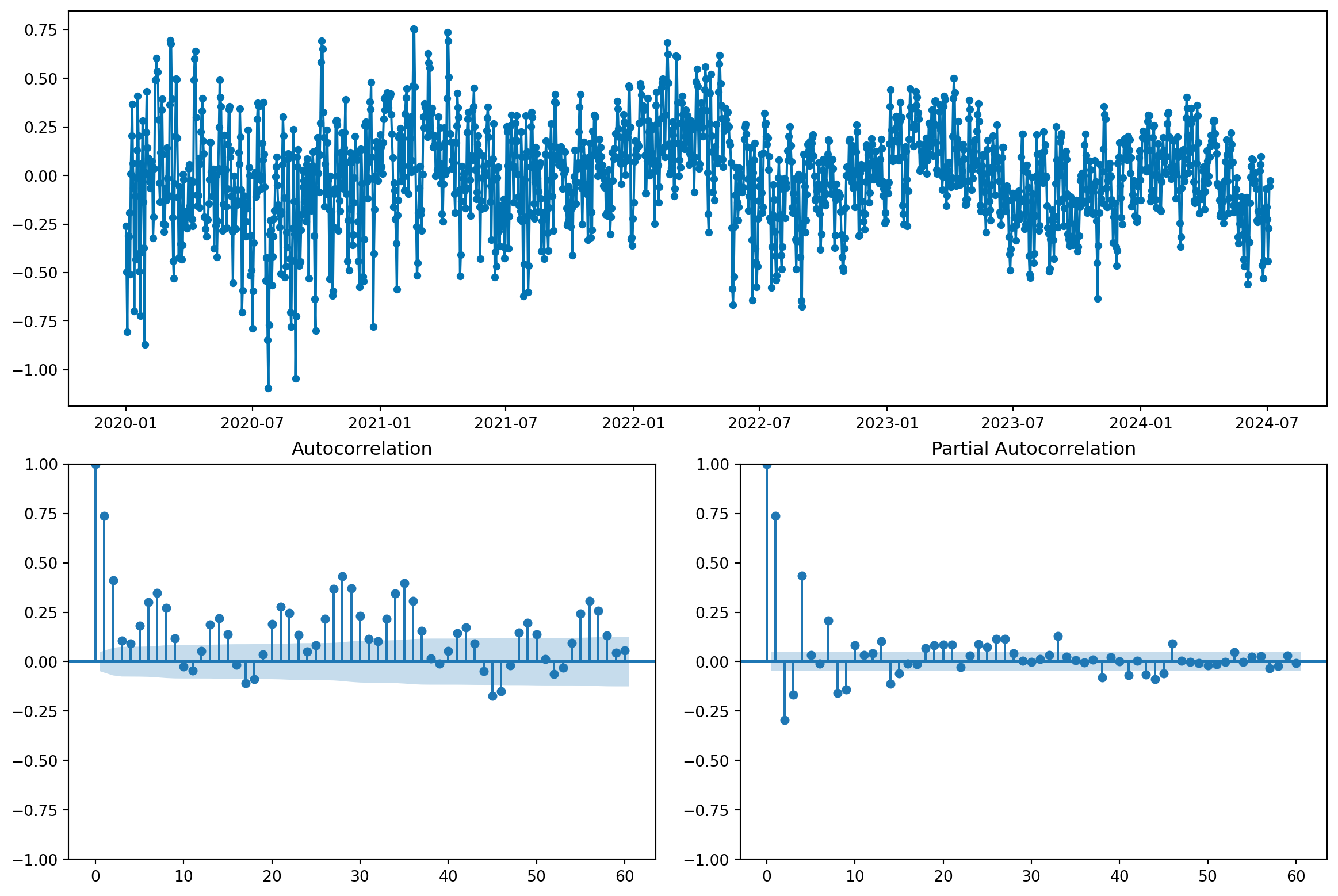

O que indica que, ao eliminar a tendencia, a informação que o passado carrega sobre o futuro diminuiu bastante. Na verdade, a existência da tendência - um efeito de longo prazo - faz com que valores passados sejam altamente correlacionados com valores futuros, e pode dar a falsa impressão de que a série é “fácil” de modelar.

3.3.1.2 Sazonalidade

Agora, usamos o Deseasonalizer para remover a sazonalidade:

deseasonalizer = LogTransformer() * Deseasonalizer(model="additive", sp=365)
deseasonalizer.fit(y_train)
y_train_deseasonalized = deseasonalizer.transform(y_train)
plot_series(y_train_log, y_train_deseasonalized, labels=["Log with seasonality", "Deseasonalized"])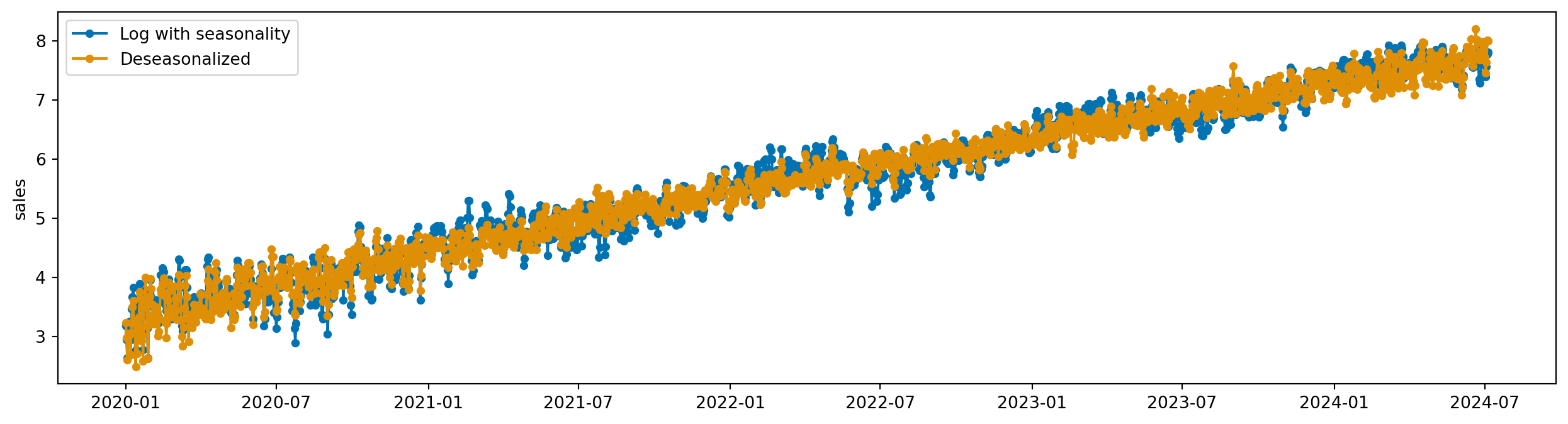

Podemos usar o Detrender e o Deseasonalizer juntos para remover ambos os componentes:

remove_components = LogTransformer() * Detrender(model="additive") * Deseasonalizer(model="additive", sp=365) 
remove_components.fit(y_train)
y_train_removed = remove_components.transform(y_train)
plot_series(y_train_log, y_train_removed, labels=["Log with seasonality", "Deseasonalized and detrended"])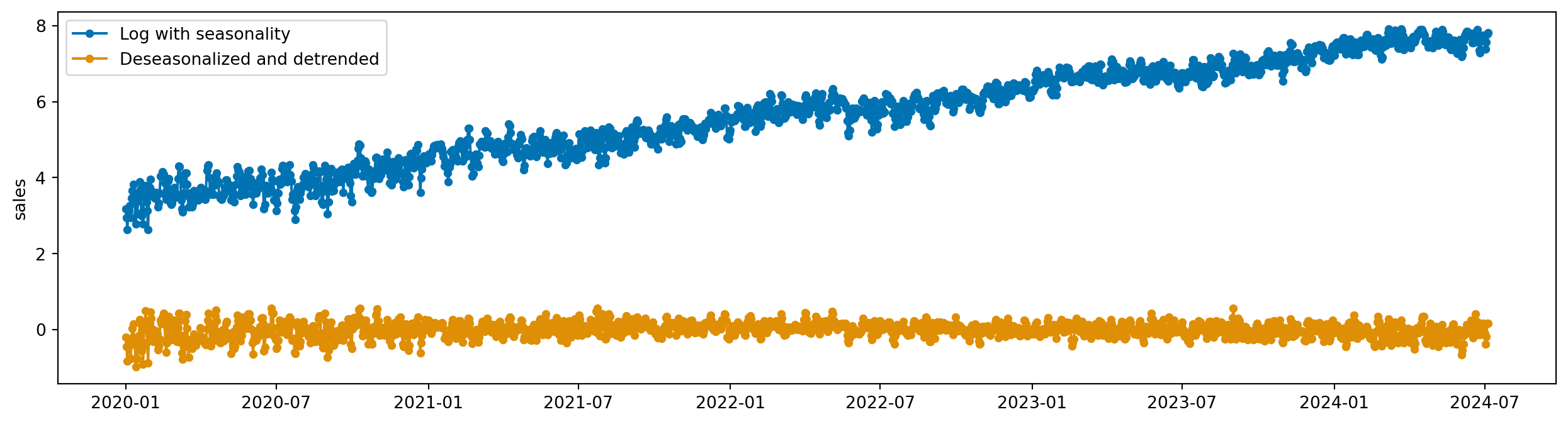

fig, _ = plot_correlations(y_train_removed, lags=60)
fig.show()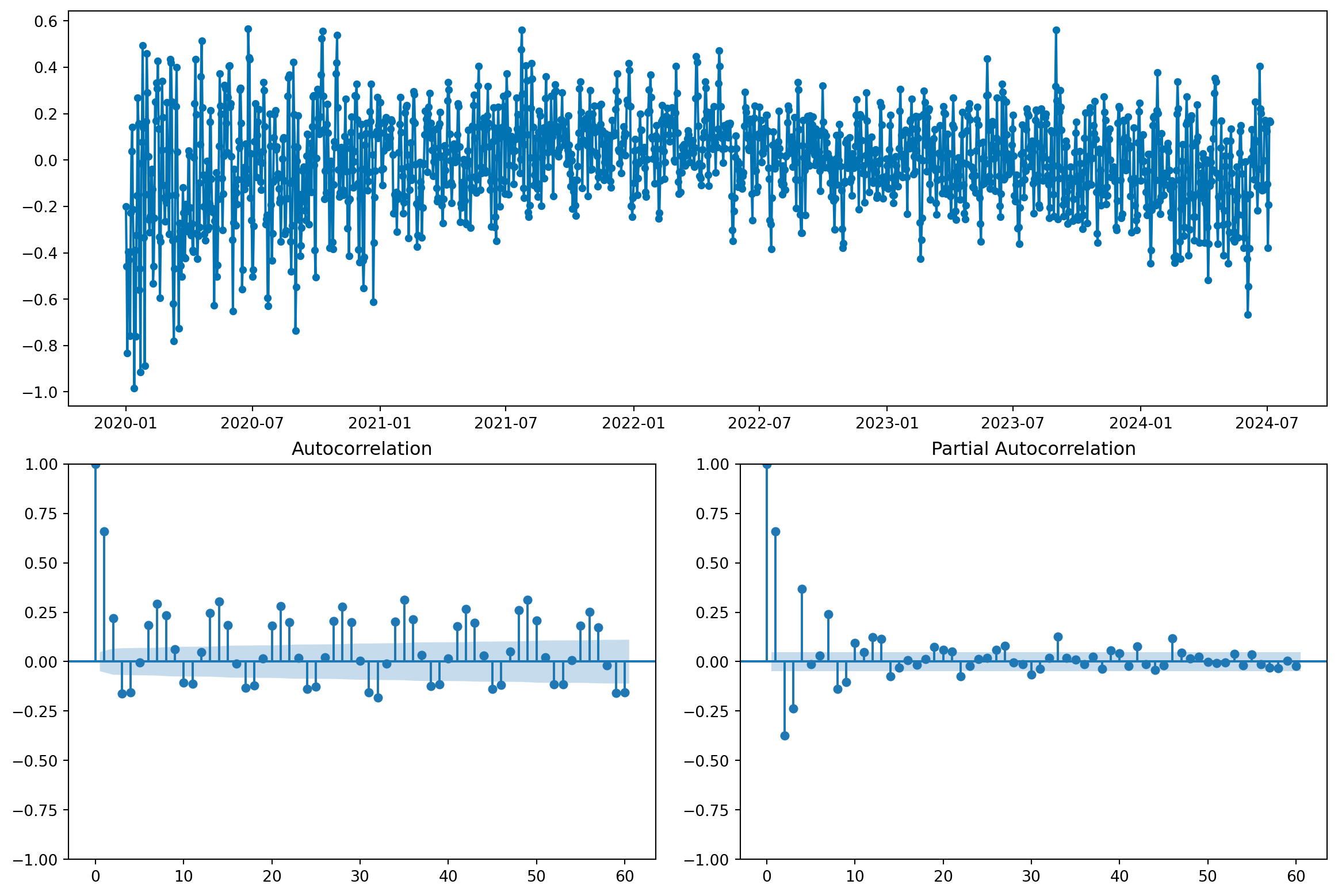

Tip

Tente adicionar mais um deseasonalizer para remover a sazonalidade semanal.

3.4 Séries estacionárias

O conceito de estacionariedade é fundamental em séries temporais. Uma série temporal é dita estacionária se suas propriedades estatísticas, como média, variância e autocovariância, são constantes ao longo do tempo, não importando a janela e quando ela é observada.

Mais precisamente, se \(Y(t)\), onde \(t\) é o indice temporal, então dizemos que ela é estacionária se:

\[ P(Y(t_{start}:t_{end})) = P(Y(t_{start}+k:t_{end}+k)), \quad \forall k, t_{start}, t_{end} \in \mathbb{Z} \]

Claramente, a série temporal que estamos analisando não é estacionária. Basta percebermos que para valores maiores de \(t\), a média e a variância são maiores.

O aumento da média da série ao longo do tempo é chamado de tendência. A tendência é um padrão de longo prazo na série temporal, e um grande desafio para previsões de longo prazo.

Existem definições mais “suaves” de estacionariedade, como a estacionariedade fraca, que requer apenas que propriedades como média e autovariância sejam constantes ao longo do tempo.

No fundo, o que nos interessa mais é ter uma série temporal que seja “fácil”de modelar. Para alguns algoritmos, como Naive, é importante que ela seja o mais próxima possível de estacionária. Veja abaixo o problema geraodo quando aplicamos o modelo Naive diretamente na série temporal original.

from sktime.forecasting.naive import NaiveForecaster

naive = NaiveForecaster(strategy="mean", window_length=24)
naive.fit(y_train)
y_pred = naive.predict(fh=y_test.index)

plot_series(y_train, y_test, y_pred, labels=["Treino", "Teste", "Previsão Naive"])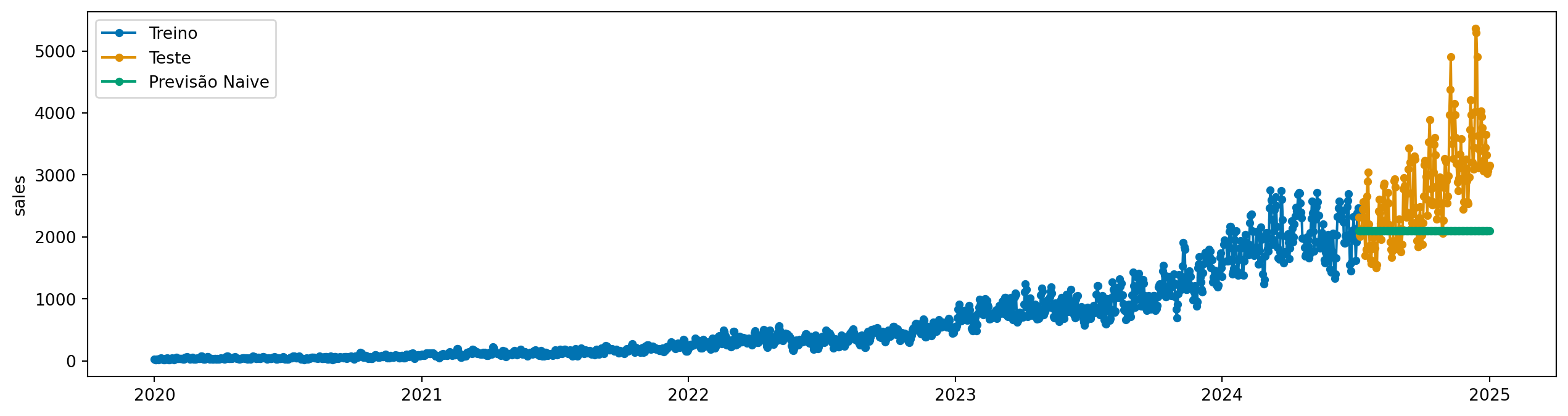

3.4.1 Diferenciação

Uma técnica simples e eficaz para lidar com séries não estacionárias é a diferenciação. Calculamos:

\[ Y'(t) = Y(t) - Y(t-1) \]

e fazemos previsões em \(Y'(t)\) ao invés de \(Y(t)\). Para obter a previsão de \(Y(t)\), precisamos fazer o processo inverso: somar a previsão de \(Y'(t)\) com o valor anterior de \(Y(t-1)\).

\[ \hat{Y(t)} = \hat{Y'}(t) + \hat{Y}(t-1), \quad \hat{Y}(0) \text{ conhecido} \]

Com sktime, isso é extremamente fácil. Aqui, vamos usar um transformador chamado Differencer.

from sktime.transformations.series.difference import Differencer
diff = Differencer()
diff.fit(y_train)

Differencer()

Please rerun this cell to show the HTML repr or trust the notebook.

y_train_diff = diff.transform(y_train)

plot_series(y_train, y_train_diff, labels=["Original", "Diferenciado"])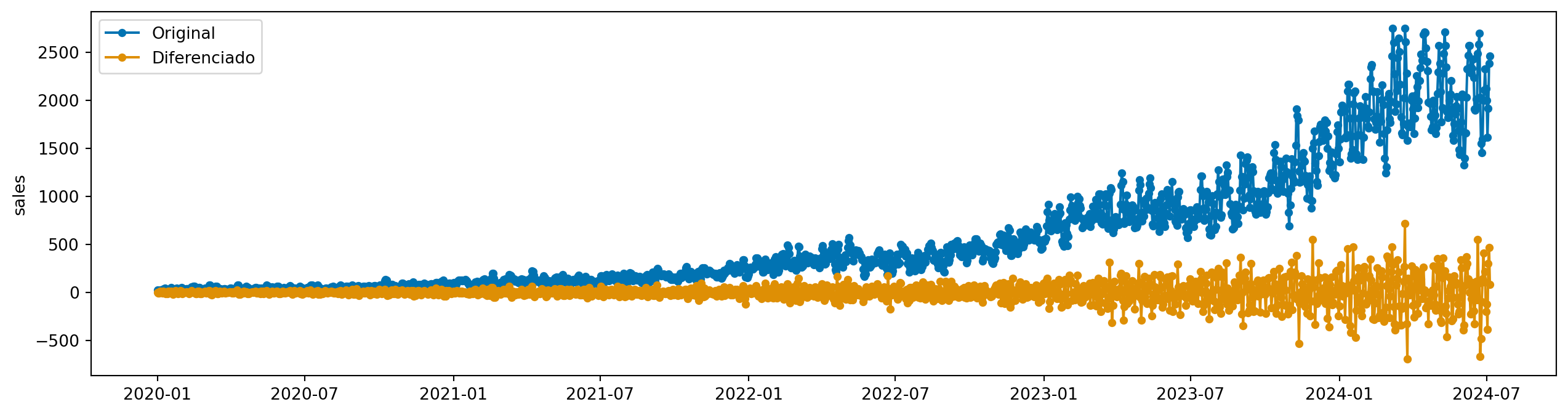

3.5 Criando um pipeline com diferenciação e Naive

Agora, podemos criar um modelo de forecasting mais complexo, composto por dois passos:

Diferenciação dos dados
Modelo Naive aplicado nos dados diferenciados

Para isso, usamos a classe TransformedTargetForecaster, que cria um pipeline de transformadores e um modelo de previsão.

from sktime.forecasting.compose import TransformedTargetForecaster

model = TransformedTargetForecaster(steps=[
    ("differencer", Differencer()),
    ("naive", NaiveForecaster(strategy="mean", window_length=24))
])
model.fit(y_train)

TransformedTargetForecaster(steps=[('differencer', Differencer()),
                                   ('naive',
                                    NaiveForecaster(strategy='mean',
                                                    window_length=24))])

Please rerun this cell to show the HTML repr or trust the notebook.

Ou apenas:

model = Differencer() * NaiveForecaster(strategy="mean", window_length=24)
model.fit(y_train)

TransformedTargetForecaster(steps=[Differencer(),
                                   NaiveForecaster(strategy='mean',
                                                   window_length=24)])

Please rerun this cell to show the HTML repr or trust the notebook.

E agora podemos prever:

y_pred = model.predict(fh=y_test.index)
plot_series(y_train, y_test, y_pred, labels=["Treino", "Teste", "Previsão Naive com diferenciação"])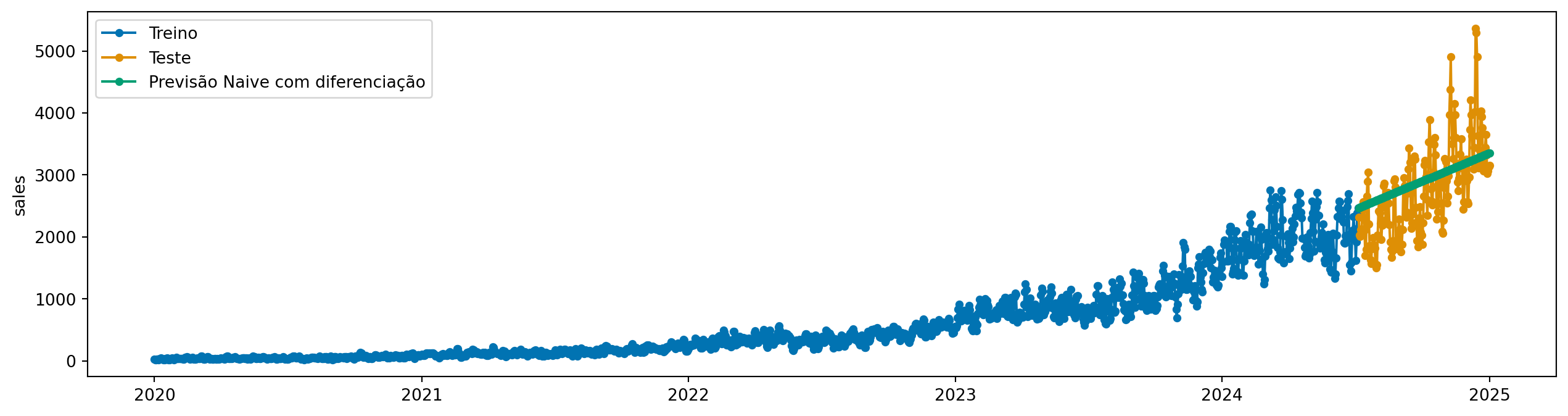

Existem ainda alguns problemas com a diferenciação. Note que a variância da série temporal diferenciada não é constante ao longo do tempo. Aqui, podemos combinar nossa transformação logarítmica com a diferenciação.

Primeiro, vamos criar um transformador que combina as duas transformações:

from sktime.transformations.compose import TransformerPipeline

log_diff = TransformerPipeline(steps=[
    ("log", LogTransformer()),
    ("diff", Differencer())
])
log_diff.fit(y_train)

TransformerPipeline(steps=[('log', LogTransformer()), ('diff', Differencer())])

Please rerun this cell to show the HTML repr or trust the notebook.

y_train_log_diff = log_diff.transform(y_train)
plot_series(y_train_log_diff, labels=["Log + Diferenciado"])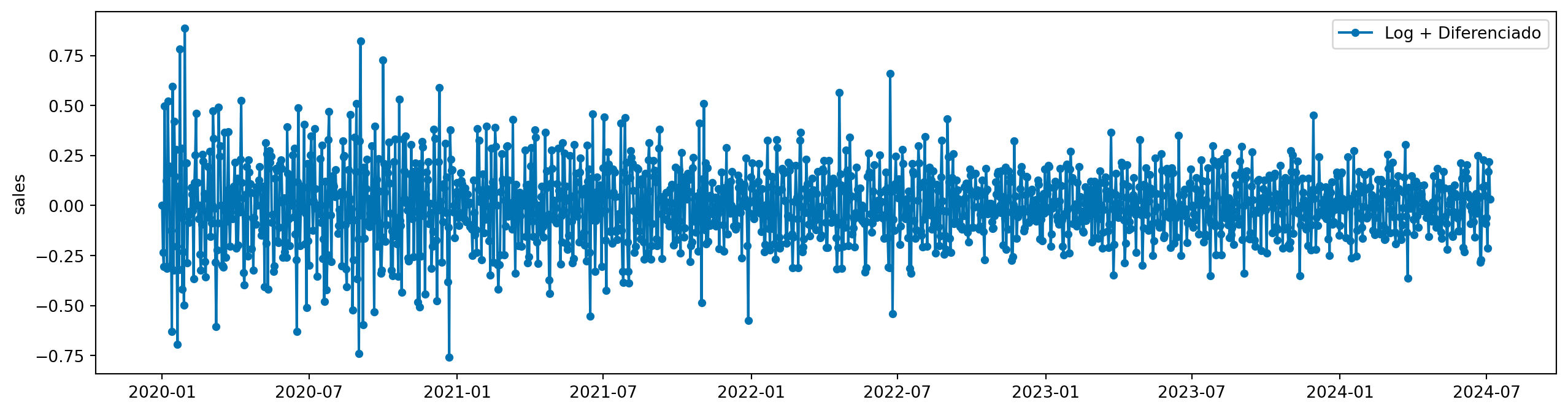

Para fazer forecast, criamos um pipeline com o transformador combinado e o modelo Naive:

model = log_diff * NaiveForecaster(strategy="mean", window_length=24)
model.fit(y_train)
y_pred = model.predict(fh=y_test.index)
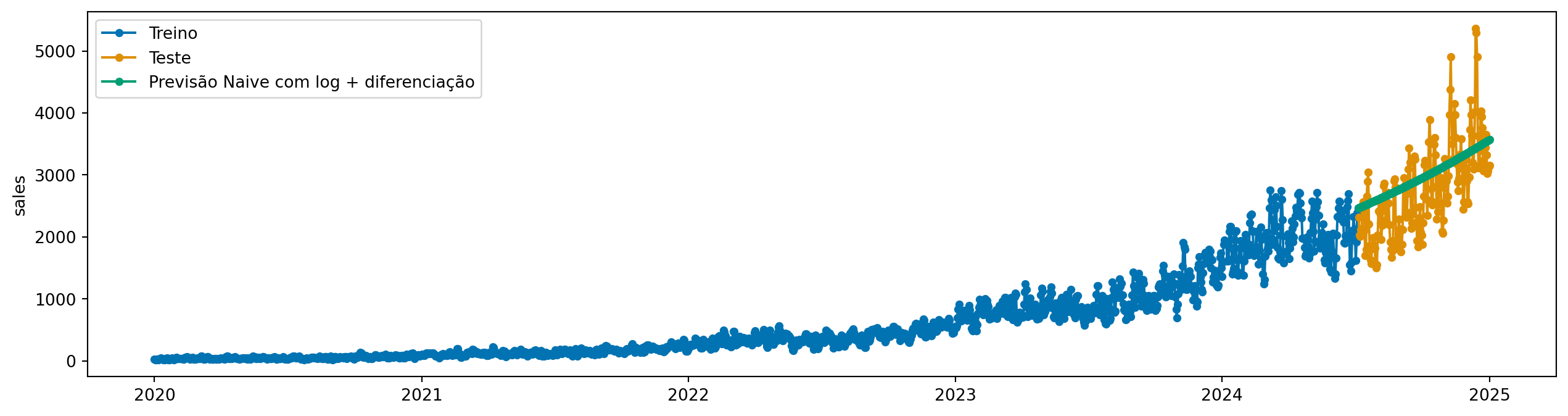
plot_series(y_train, y_test, y_pred, labels=["Treino", "Teste", "Previsão Naive com log + diferenciação"])