5 Métricas e cross-validation

Até então, vimos como criar modelos de séries temporais e avaliamos qualitativamente seu desempenho, em apenas uma simples divisão treino-teste. Agora, vamos explorar como avaliar modelos de séries temporais de forma mais robusta, utilizando métricas específicas e técnicas de validação cruzada adaptadas para dados temporais.

5.1 Métricas

Primeiro vamos baixar os dados e criar um modelo simples.

import matplotlib.pyplot as plt
from tsbook.datasets.retail import SyntheticRetail
from sktime.utils.plotting import plot_series
from sktime.forecasting.naive import NaiveForecaster

dataset = SyntheticRetail("univariate")
y_train, y_test = dataset.load("y_train", "y_test")

# Predict
model = NaiveForecaster(strategy="last")
model.fit(y_train)
y_pred = model.predict(fh=y_test.index)

Para avaliar o desempenho de modelos de séries temporais, existem diversas métricas que podem ser utilizadas.

Duas métricas básicas são:

Mean Absolute Error (MAE): Média dos erros absolutos entre as previsões e os valores reais. \[ MAE = \frac{1}{h} \sum_{t=T+1}^{T+h} |y_t - \hat{y}_t| \]

from sktime.performance_metrics.forecasting import MeanAbsoluteError

metric = MeanAbsoluteError()
metric(y_true=y_test, y_pred=y_pred)

np.float64(614.9555555555555)

Mean Squared Error (MSE): Média dos erros quadráticos entre as previsões e os valores reais.

\[ MSE = \frac{1}{h} \sum_{t=T+1}^{T+h} (y_t - \hat{y}_t)^2 \]

from sktime.performance_metrics.forecasting import MeanSquaredError

metric = MeanSquaredError()
metric(y_true=y_test, y_pred=y_pred)

np.float64(633516.4555555555)

No entanto, essas métricas não levam em consideração a escala dos dados, o que pode ser um problema ao comparar desempenho entre diferentes séries temporais, e também na comunicação dos resultados para stakeholders.

Em muitos meios, é comum usar métricas que eliminam o fator escala, como:

Mean Absolute Percentage Error (MAPE): Média dos erros percentuais absolutos entre as previsões e os valores reais.

\[ MAPE = \frac{1}{h} \sum_{t=T+1}^{T+h} \left| \frac{y_t - \hat{y}_t}{y_t} \right| \]

from sktime.performance_metrics.forecasting import MeanAbsolutePercentageError

metric = MeanAbsolutePercentageError()
metric(y_true=y_test, y_pred=y_pred)

np.float64(0.21289989268196857)

Symmetric Mean Absolute Percentage Error (sMAPE): Média dos erros percentuais absolutos simétricos entre as previsões e os valores reais.

metric = MeanAbsolutePercentageError(symmetric=True)
metric(y_true=y_test, y_pred=y_pred)

np.float64(0.22352456623275035)

\[ sMAPE = \frac{1}{h} \sum_{t=T+1}^{T+h} \frac{|y_t - \hat{y}_t|}{(|y_t| + |\hat{y}_t|)/2} \]

Essas métricas, no entanto, apresentam seus próprios problemas. Note que os valores podem ser exageradamente alto quando o denominador é próximo de zero. Ou seja, o MAPE e sMAPE podem ser problemáticos quando a série temporal contém valores próximos de zero.

Outro tema é que essas métricas não consideram a dificuldade da série. Por exemplo, 5% de erro pode ser muito em uma série, e pouco em outra. Para isso, foram propostas métricas “escalas”:

Mean Absolute Scaled Error (MASE): dividimos o erro absoluto pelo erro absoluto médio de um naive nos dados de treino. Se:

\[ e_{naive} = \frac{1}{T-1} \sum_{t=2}^{T} |y_t - y_{t-1}| \]

são os erros nos dados de treino, então:

\[ MASE = \frac{1}{h} \sum_{t=T+1}^{T+h} \frac{|y_t - \hat{y}_t|}{e_{naive}} \]

from sktime.performance_metrics.forecasting import MeanAbsoluteScaledError

metric = MeanAbsoluteScaledError()
metric(y_true=y_test, y_pred=y_pred, y_train=y_train)

np.float64(10.123559926834387)

Mean Squared Scaled Error (MSSE): dividimos o erro quadrático pelo quadrado de \(e_{naive}\).

\[ MSSE = \frac{1}{h} \sum_{t=T+1}^{T+h} \frac{(y_t - \hat{y}_t)^2}{e_{naive}^2} \]

from sktime.performance_metrics.forecasting import MeanSquaredScaledError

metric = MeanSquaredScaledError()
metric(y_true=y_test, y_pred=y_pred, y_train=y_train)

np.float64(57.07280843131573)

5.2 Cross-validation para séries temporais

Em um cross-validation, nossa intenção é estimar corretamente o erro de generalização do modelo, ou seja, o erro que o modelo terá em dados futuros.

\[ \mathbb{E}[L(Y, \hat{Y})] \]

Onde a média é sobre a distribuição que mais representa o que será visto em produção.

Tipicamente, fazemos back-testing com dois tipos de janelas:

Sliding window: a janela de treino tem tamanho fixo, e “desliza” ao longo do tempo. A cada passo, o modelo é re-treinado com os dados mais recentes.

from sktime.utils.plotting import plot_windows

from sktime.split import SlidingWindowSplitter

sliding_window_cv = SlidingWindowSplitter(
    window_length=365 * 3, step_length=100, fh=list(range(1, 90 + 1))
)
plot_windows(cv=sliding_window_cv, y=y_train)
plt.show()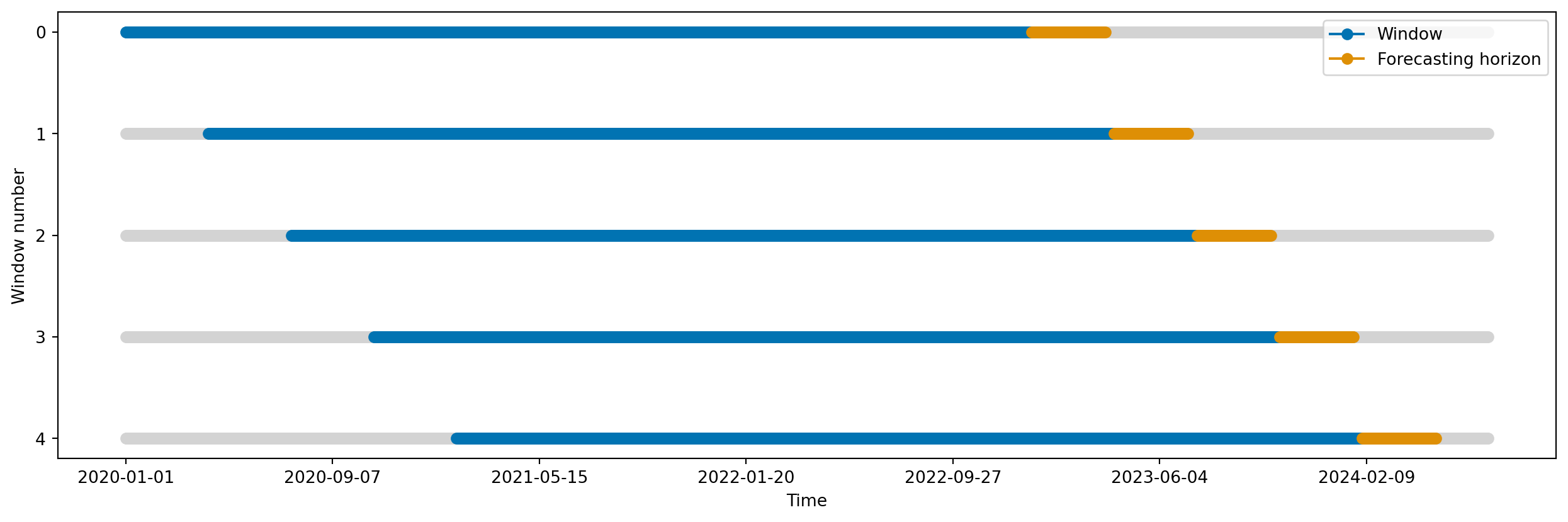

Expanding window: a janela de treino começa com um tamanho mínimo, e vai aumentando ao longo do tempo, incluindo todos os dados anteriores. A cada passo, o modelo é re-treinado com todos os dados disponíveis até aquele ponto.

from sktime.split import ExpandingWindowSplitter



expanding_window_cv = ExpandingWindowSplitter(
    initial_window=365 * 3, step_length=100, fh=list(range(1, 90 + 1))
)
plot_windows(cv=expanding_window_cv, y=y_train)
plt.show()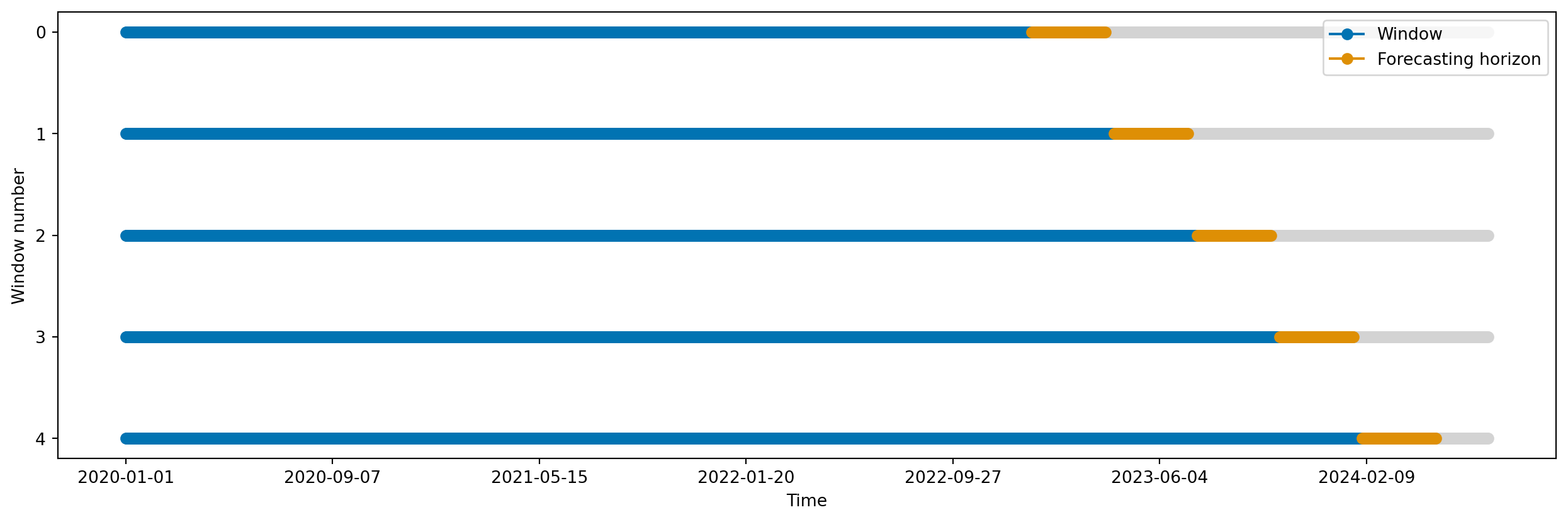

Qual escolher? Bom, escolha o que mais representa o que você espera ver em produção.

5.3 Executando o cross-validation

Para executar cross-validation, usamos a função evaluate, que recebe o modelo, o esquema de cross-validation, os dados, e a métrica a ser usada.

from sktime.forecasting.model_evaluation import evaluate
from sktime.performance_metrics.forecasting import MeanAbsoluteScaledError
from sktime.forecasting.naive import NaiveForecaster

model = NaiveForecaster(strategy="last")

evaluate(
    forecaster=model,
    cv=expanding_window_cv,
    y=y_train,
    X=None, # Veremos na próxima seçao!
    scoring=MeanAbsoluteScaledError(),
    error_score="raise",
    return_data=True,
)

	test_MeanAbsoluteScaledError	fit_time	pred_time	len_train_window	cutoff	y_train	y_test	y_pred
0	12.834619	0.004481	0.010213	1095	2022-12-30	sales date 2020-01-01...	sales date 2022-12-31...	sales 2022-12-31 458.0 2023-01-01...
1	3.808715	0.004078	0.009949	1195	2023-04-09	sales date 2020-01-01...	sales date 2023-04-10...	sales 2023-04-10 866.0 2023-04-11...
2	8.057811	0.004054	0.009979	1295	2023-07-18	sales date 2020-01-01...	sales date 2023-07-19...	sales 2023-07-19 748.0 2023-07-20...
3	7.854351	0.004104	0.010242	1395	2023-10-26	sales date 2020-01-01...	sales date 2023-10-27...	sales 2023-10-27 1229.0 2023-10-...
4	5.956618	0.004057	0.009689	1495	2024-02-03	sales date 2020-01-01...	sales date 2024-02-04...	sales 2024-02-04 1915.0 2024-02-...