8 Dados em painel (multi-series)

Em muitas aplicações, não temos acesso a uma única série temporal, mas sim a um conjunto de séries temporais relacionadas. Isso é comum em cenários como vendas de produtos em diferentes lojas, consumo de energia em diferentes regiões, etc. Esses dados são chamados de dados em painel.

Uma ideia poderosa é aproveitar a similaridade entre as séries para melhorar as previsões. Chamamos de modelos globais os modelos capazes de aprender padrões comuns entre as séries, ao contrário dos modelos locais que aprendem apenas com uma única série.

A maioria dos modelos clássicos de séries temporais são locais. Modelos globais são, em geral, baseados em modelos tabulares de ML ou deep learning. Segundo competições de séries temporais, como a M5, em forecasts de painel os modelos globais são os que apresentam melhor desempenho (Makridakis, Spiliotis, and Assimakopoulos 2022).

8.1 Acessando os dados

Aqui, vamos usar o dataset sintético que vimos antes, mas agora teremos acesso às várias séries temporais que compõe o total.

Esse dataset é feito para simular um caso de varejo, onde temos vendas diárias de vários produtos:

Code

import pandas as pd
import matplotlib.pyplot as plt

from sktime.utils.plotting import plot_series

from tsbook.datasets.retail import SyntheticRetail
dataset = SyntheticRetail("panel")
y_train, X_train, y_test, X_test = dataset.load(
    "y_train", "X_train", "y_test", "X_test"
)

Note que, para dados em painel, os dataframes possuem mais um nível de índice, que identifica a série temporal a que cada observação pertence:

display(X_train)

		promo
sku_id	date
0	2020-01-01	0.0
	2020-01-02	0.0
	2020-01-03	0.0
	2020-01-04	0.0
	2020-01-05	0.0
...	...	...
24	2024-07-01	1.0
	2024-07-02	0.0
	2024-07-03	0.0
	2024-07-04	0.0
	2024-07-05	0.0

41200 rows × 1 columns

Podemos visualizar algumas séries. Vemos que há mais zeros nesse dataset, em comparação ao que usamos antes.

from sktime.utils.plotting import plot_series

fig, ax = plt.subplots(figsize=(10, 4))
y_train.unstack(level=0).droplevel(0, axis=1).iloc[:, [0,10]].plot(ax=ax, alpha=0.7)
plt.show()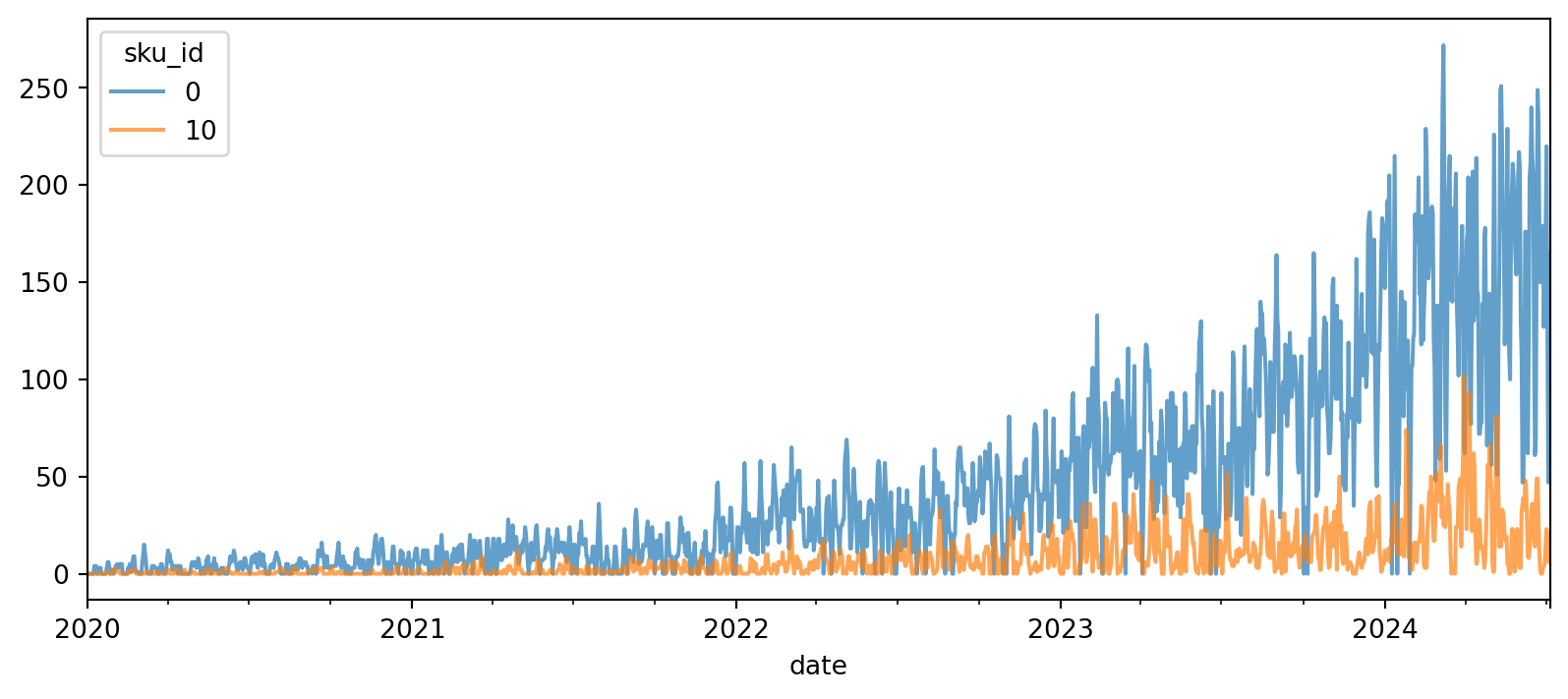

8.1.1 Pandas e multi-índices

Para trabalhar com essas estruturas de dados, é importante revisar algumas operações do pandas.

y_train.index.get_level_values(-1)

PeriodIndex(['2020-01-01', '2020-01-02', '2020-01-03', '2020-01-04',
             '2020-01-05', '2020-01-06', '2020-01-07', '2020-01-08',
             '2020-01-09', '2020-01-10',
             ...
             '2024-06-26', '2024-06-27', '2024-06-28', '2024-06-29',
             '2024-06-30', '2024-07-01', '2024-07-02', '2024-07-03',
             '2024-07-04', '2024-07-05'],
            dtype='period[D]', name='date', length=41200)

As seguintes operações são bem úteis para trabalhar com multi-índices:

y_train.index

MultiIndex([( 0, '2020-01-01'),
            ( 0, '2020-01-02'),
            ( 0, '2020-01-03'),
            ( 0, '2020-01-04'),
            ( 0, '2020-01-05'),
            ( 0, '2020-01-06'),
            ( 0, '2020-01-07'),
            ( 0, '2020-01-08'),
            ( 0, '2020-01-09'),
            ( 0, '2020-01-10'),
            ...
            (24, '2024-06-26'),
            (24, '2024-06-27'),
            (24, '2024-06-28'),
            (24, '2024-06-29'),
            (24, '2024-06-30'),
            (24, '2024-07-01'),
            (24, '2024-07-02'),
            (24, '2024-07-03'),
            (24, '2024-07-04'),
            (24, '2024-07-05')],
           names=['sku_id', 'date'], length=41200)

Acessar valores únicos no primeiro nivel (nível 0, mais à esquerda):

y_train.index.get_level_values(0).unique()

Index([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17,
       18, 19, 20, 21, 22, 23, 24],
      dtype='int64', name='sku_id')

Selecionar uma série específica (nível 0 igual a 0):

y_train.loc[0]

	sales
date
2020-01-01	0
2020-01-02	0
2020-01-03	0
2020-01-04	0
2020-01-05	0
...	...
2024-07-01	220
2024-07-02	128
2024-07-03	47
2024-07-04	73
2024-07-05	165

1648 rows × 1 columns

Aqui, podemos usar pd.IndexSlice para selecionar várias séries ao mesmo tempo. Note que pd.IndexSlice é passado diretamente para .loc:

y_train.loc[pd.IndexSlice[[0,2], :]]

		sales
sku_id	date
0	2020-01-01	0
	2020-01-02	0
	2020-01-03	0
	2020-01-04	0
	2020-01-05	0
...	...	...
2	2024-07-01	125
	2024-07-02	185
	2024-07-03	179
	2024-07-04	210
	2024-07-05	236

3296 rows × 1 columns

Agora, para selecionar o horizonte de forecasting, temos que chamar unique:

fh = y_test.index.get_level_values(1).unique()

fh

PeriodIndex(['2024-07-06', '2024-07-07', '2024-07-08', '2024-07-09',
             '2024-07-10', '2024-07-11', '2024-07-12', '2024-07-13',
             '2024-07-14', '2024-07-15',
             ...
             '2024-12-23', '2024-12-24', '2024-12-25', '2024-12-26',
             '2024-12-27', '2024-12-28', '2024-12-29', '2024-12-30',
             '2024-12-31', '2025-01-01'],
            dtype='period[D]', name='date', length=180)

8.2 Upcasting automático

Nem todos modelos suportam nativamente dados em painel. Por exemplo, exponential smoothing. Aqui, temos uma boa notícia: sem linhas extras necessárias. O sktime faz upcasting automático para dados em painel ao usar estimadores do sktime.

from sktime.forecasting.naive import NaiveForecaster


naive_forecaster = NaiveForecaster(strategy="last", window_length=1)
naive_forecaster.fit(y_train)
y_pred_naive = naive_forecaster.predict(fh=fh)

y_pred_naive

		sales
sku_id	date
0	2024-07-06	165.0
	2024-07-07	165.0
	2024-07-08	165.0
	2024-07-09	165.0
	2024-07-10	165.0
...	...	...
24	2024-12-28	209.0
	2024-12-29	209.0
	2024-12-30	209.0
	2024-12-31	209.0
	2025-01-01	209.0

4500 rows × 1 columns

Internamente, o sktime cria um clone do estimador para cada série nos dados em painel. Em seguida, cada clone é treinado com a série correspondente. Isso é feito de forma transparente para usuário, mas sem exigir esforço.

O atributo forecasters_ armazena um DataFrame com os estimatores de cada série.

naive_forecaster.forecasters_.head()

	forecasters
0	NaiveForecaster(window_length=1)
1	NaiveForecaster(window_length=1)
2	NaiveForecaster(window_length=1)
3	NaiveForecaster(window_length=1)
4	NaiveForecaster(window_length=1)

É dificil explicar o quanto isso é extremamente útil para código limpo e prototipagem rápida. Foi um dos motivos que me levaram a usar o sktime.

8.3 Métricas

Agora que temos várias séries, precisamos explicar como calcular métricas de avaliação. O sktime oferece duas opções para isso, como argumentos na criação da métrica:

multilevel="uniform_average_time" para calcular a média das séries temporais no painel.
multilevel="raw_values" para obter o erro por série.

from sktime.performance_metrics.forecasting import MeanSquaredScaledError

metric = MeanSquaredScaledError(multilevel="uniform_average_time")

metric(y_true=y_test, y_pred=y_pred_naive, y_train=y_train)

np.float64(19.047949908747597)

Na prática, as métricas que a sua aplicação exige podem ser diferentes. Por exemplo, as séries temporais podem ter diferentes importâncias, e você pode querer ponderar as métricas de acordo.

Para isso, é possível criar uma métrica customizada no sktime, mas não entraremos nesse mérito aqui.

8.4 Modelos globais de Machine Learning

Quando vimos como usar modelos de Machine Learning para forecasting, já mencionamos como é necessário traduzir o problema de séries temporais para um problema de regressão tradicional.

No caso de dados em painel, também podemos usar essa abordagem, mas agora aproveitando todas as séries temporais para treinar um único modelo global.

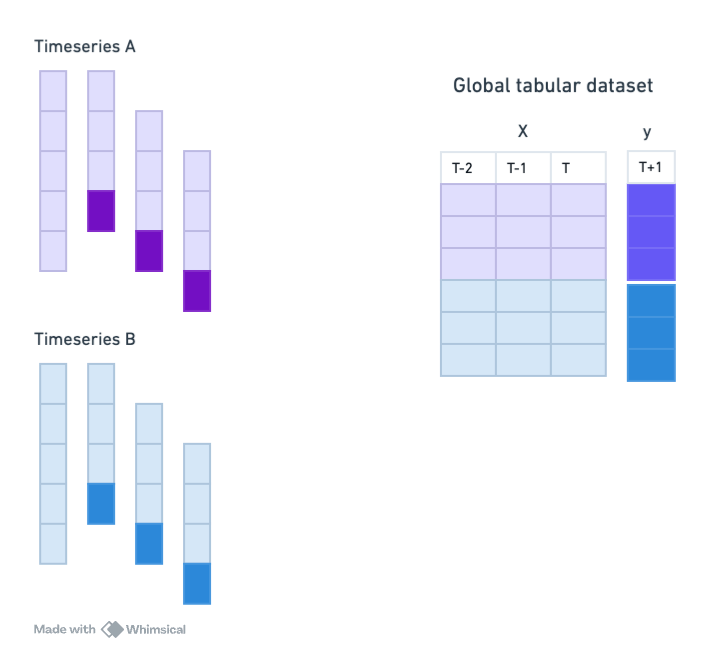
Abaixo, vamos comparar um LightGBM global com um local. Veremos o seguinte: o modelo local é melhor que o modelo global, se não processarmos os dados corretamente para o modelo global aproveitar as similaridades entre as séries!

from tsbook.forecasting.reduction import ReductionForecaster
from lightgbm import LGBMRegressor

global_forecaster1 = ReductionForecaster(
    LGBMRegressor(n_estimators=100, verbose=-1, random_state=42),
    window_length=30,
)

global_forecaster1.fit(y_train, X_train)

ReductionForecaster(estimator=LGBMRegressor(random_state=42, verbose=-1),
                    window_length=30)

Please rerun this cell to show the HTML repr or trust the notebook.

y_pred_global1 = global_forecaster1.predict(fh=fh, X=X_test)

fig, ax = plt.subplots(figsize=(10, 4))
y_train.loc[10, "sales"].plot(ax=ax, label="Treino")
y_test.loc[10, "sales"].plot(ax=ax, label="Teste")
y_pred_global1.loc[10, "sales"].plot(ax=ax, label="Global 1")
plt.legend()
plt.show()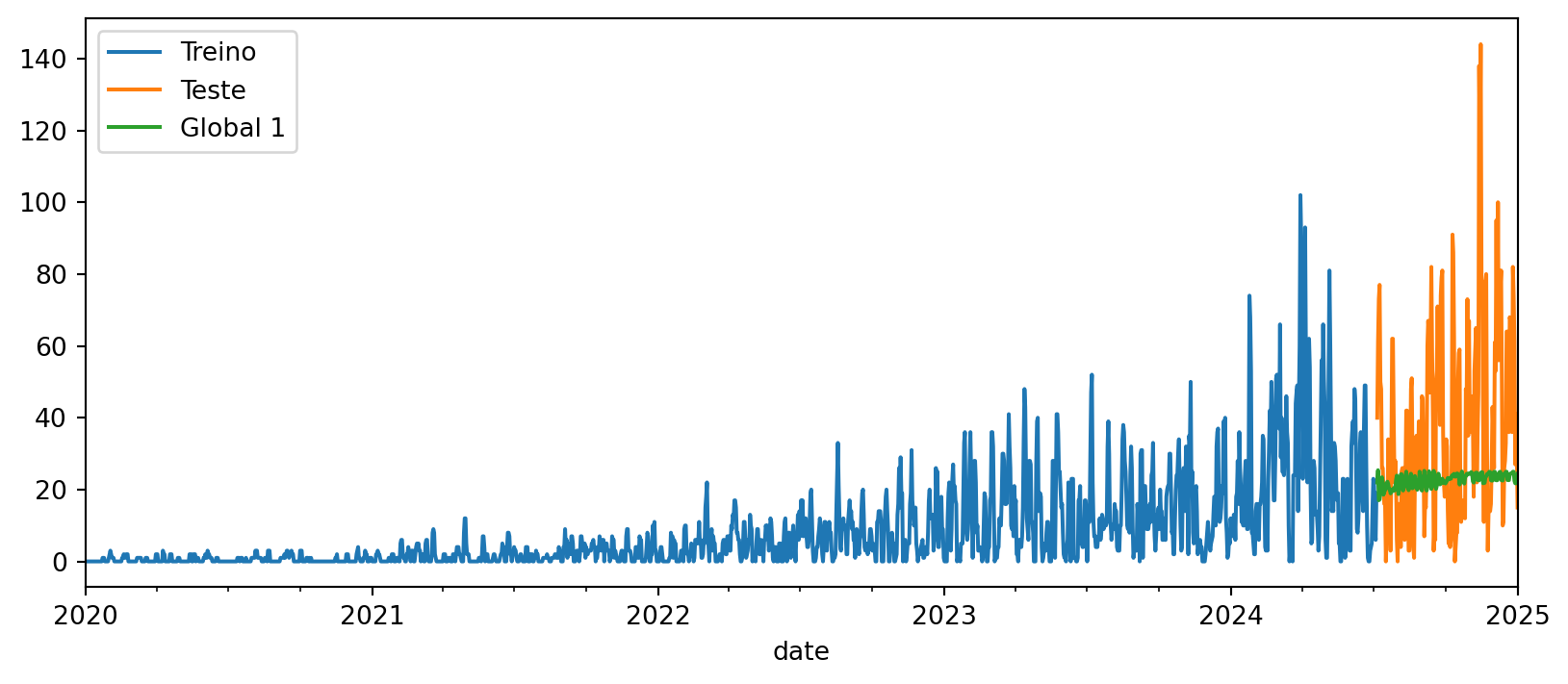

Para forçar que um modelo global funcione como um modelo local, podemos usar ForecastByLevel, que cria um modelo separado para cada série temporal, mesmo quando o estimador suporta dados em painel.

from sktime.forecasting.compose import ForecastByLevel

local_forecaster1 = ForecastByLevel(global_forecaster1, groupby="local")

local_forecaster1.fit(y_train, X=X_train)

ForecastByLevel(forecaster=ReductionForecaster(estimator=LGBMRegressor(random_state=42, verbose=-1),
                                               window_length=30))

Please rerun this cell to show the HTML repr or trust the notebook.

y_pred_local1 = local_forecaster1.predict(fh=fh, X=X_test)

err_global1 = metric(y_true=y_test, y_pred=y_pred_global1, y_train=y_train)
err_local1 = metric(y_true=y_test, y_pred=y_pred_local1, y_train=y_train)

errors = pd.DataFrame(
    {
        "Global (1)": [err_global1],
        "Local (1)": [err_local1],
    },
    index=["MSE"],
)

8.5 Preprocessamento e engenharia de features

Sabemos como preprocessar séries temporais univariadas para melhorar o desempenho dos modelos de ML. Aplicamos da mesma maneira que fizemos anteriormente o Differencer, com objetivo de remover tendências.

from sktime.transformations.series.difference import Differencer

global_forecaster2 = Differencer() * global_forecaster1
global_forecaster2.fit(y_train, X_train)

TransformedTargetForecaster(steps=[Differencer(),
                                   ReductionForecaster(estimator=LGBMRegressor(random_state=42, verbose=-1),
                                                       window_length=30)])

Please rerun this cell to show the HTML repr or trust the notebook.

y_pred_global2 = global_forecaster2.predict(fh=fh, X=X_test)
metric_global2 = metric(y_true=y_test, y_pred=y_pred_global2, y_train=y_train)

E agora sua versão local:

local_forecaster2 = ForecastByLevel(global_forecaster2, groupby="local")
local_forecaster2.fit(y_train, X=X_train)

y_pred_local2 = local_forecaster2.predict(fh=fh, X=X_test)
metric_local2 = metric(y_true=y_test, y_pred=y_pred_local2, y_train=y_train)

Agora, podemos comparar:

errors["Global (2)"] = metric_global2
errors["Local (2)"] = metric_local2

errors

	Global (1)	Local (1)	Global (2)	Local (2)
MSE	34.451879	23.191404	26.580076	57.205596

Note como já superamos o modelo global incial. Isso é para destacar que é essencial realizar um bom preprocessamento e engenharia de features para que modelos de Machine Learning tenham bom desempenho em dados em painel.

8.5.1 Normalização por janela

Agora, vamos usar a normalização por janela, que é especialmente útil em dados em painel, onde as séries podem ter diferentes escalas.

global_forecaster3 = global_forecaster1.clone().set_params(
    normalization_strategy="divide_mean"
)

global_forecaster3.fit(y_train, X_train)

ReductionForecaster(estimator=LGBMRegressor(random_state=42, verbose=-1),
                    normalization_strategy='divide_mean', window_length=30)

Please rerun this cell to show the HTML repr or trust the notebook.

# Predict
y_pred_global3 = global_forecaster3.predict(fh=fh, X=X_test)

# Métrica
metric_global3 = metric(y_true=y_test, y_pred=y_pred_global3, y_train=y_train)

errors["Global 3 (window norm)"] = metric_global3

display(errors)

	Global (1)	Local (1)	Global (2)	Local (2)	Global 3 (window norm)
MSE	34.451879	23.191404	26.580076	57.205596	16.445518

Vemos que resultados são ainda melhores!

8.5.2 Pipelines de features exógenas

Podemos ajudar o modelo a capturar sazonalidades adicionando features de Fourier como features exógenas.

Usamos ** para criar um pipeline aplicado sobre as features exógenas:

from sktime.transformations.series.fourier import FourierFeatures

fourier_features = FourierFeatures(
    sp_list=[365.25, 365.25 / 12], fourier_terms_list=[1, 1], freq="D"
)

global_forecaster4 = fourier_features**global_forecaster3
global_forecaster4.fit(y_train, X_train)

ForecastingPipeline(steps=[FourierFeatures(fourier_terms_list=[1, 1], freq='D',
                                           sp_list=[365.25, 30.4375]),
                           ReductionForecaster(estimator=LGBMRegressor(random_state=42, verbose=-1),
                                               normalization_strategy='divide_mean',
                                               window_length=30)])

Please rerun this cell to show the HTML repr or trust the notebook.

y_pred_global4 = global_forecaster4.predict(fh=fh, X=X_test)
metric_global4 = metric(y_true=y_test, y_pred=y_pred_global4, y_train=y_train)

errors["Global 4 (fourier)"] = metric_global4
errors

	Global (1)	Local (1)	Global (2)	Local (2)	Global 3 (window norm)	Global 4 (fourier)
MSE	34.451879	23.191404	26.580076	57.205596	16.445518	15.749969

8.6 Agrupamento + Modelos globais

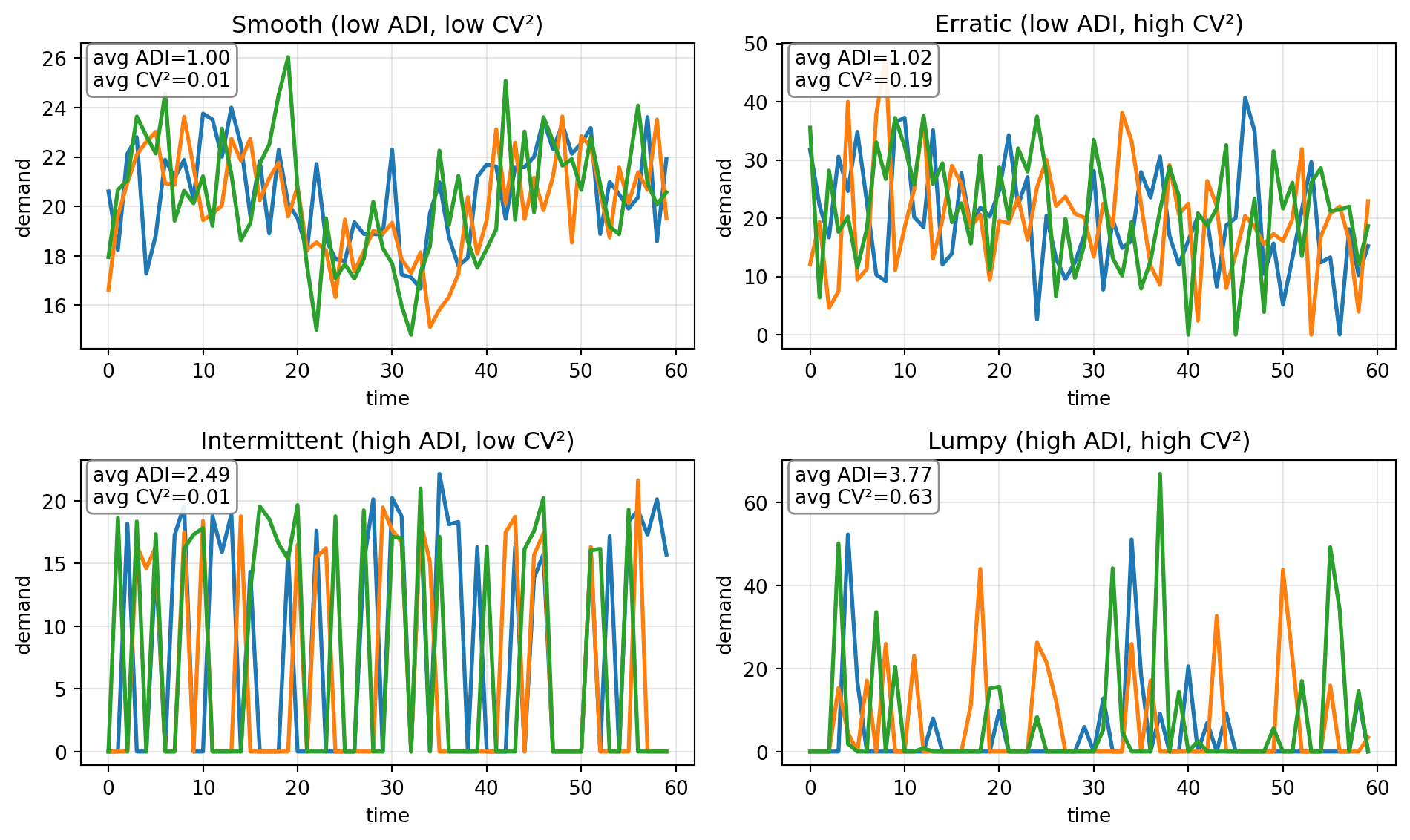
Uma técnica muito adotada é fazer modelos globais por clusters de séries temporais similares.

Uma maneira de categorizar é usando ADI (Average Demand Interval) e CV² (squared Coefficient of Variation). O componente ADI é calculado como o percentual de períodos com demanda (y>0), e \(CV^2\) é o quadrado do coeficiente de variação das demandas positivas.

Categoria	ADI	CV²	Padrão típico	Exemplos
Suave (Smooth)	≤ 1,32	≤ 0,49	Demanda contínua e estável	Itens de consumo diário, alimentos
Errática (Erratic)	≤ 1,32	> 0,49	Demanda contínua, porém muito variável	Moda, eletrônicos
Intermitente (Intermittent)	> 1,32	≤ 0,49	Muitos períodos sem venda, mas valores estáveis quando ocorre	Peças de reposição, ferramentas
Irregular (Lumpy)	> 1,32	> 0,49	Muitos períodos com zero e valores muito variáveis quando há demanda	Equipamentos caros, sobressalentes grandes

from sktime.forecasting.compose import GroupbyCategoryForecaster
from sktime.transformations.series.adi_cv import ADICVTransformer

# TODO: customize yours!
group_forecaster = GroupbyCategoryForecaster(
    forecasters =
        {"smooth": global_forecaster3.clone(),
        "erratic": global_forecaster3.clone(),
        "intermittent": global_forecaster3.clone(),
        "lumpy": global_forecaster3.clone(),
        },
    transformer=ADICVTransformer(features=["class"],))


group_forecaster.fit(y_train, X_train)

y_pred_group = group_forecaster.predict(fh=fh, X=X_test)
metric_group = metric(y_true=y_test, y_pred=y_pred_group, y_train=y_train)

metric_group

np.float64(46.754957705810234)

Although it did not perform better than the best global model in this synthetic example, in real-world scenarios this approach can be very effective, particularly when there are large samples for each category, allowing the model to learn specific patterns for each group of series.

In addition, this can be useful when there are computation constraints, as training multiple smaller models for each cluster can be more efficient than training a single large global model.

8.7 Resumo

Aqui, vimos como trabalhar com dados em painel (multi-series) usando o sktime. Vimos, especialmente, como criar modelos globais de Machine Learning que aproveitam as similaridades entre as séries para melhorar o desempenho das previsões. Também destacamos a importância do preprocessamento e da engenharia de features para obter bons resultados com esses modelos.

Para uma análise mais aprofundada, recomendo o artigo de (Montero-Manso and Hyndman 2021), que discute princípios para forecasting em dados em painel usando modelos globais de Machine Learning.

Makridakis, Spyros, Evangelos Spiliotis, and Vassilios Assimakopoulos. 2022. “M5 Accuracy Competition: Results, Findings, and Conclusions.” International Journal of Forecasting 38 (4): 1346–64.

Montero-Manso, Pablo, and Rob J Hyndman. 2021. “Principles and Algorithms for Forecasting Groups of Time Series: Locality and Globality.” International Journal of Forecasting 37 (4): 1632–53.